COMPUTING, COGNITION AND

INFORMATION COMPRESSION

J Gerard Wolff

January 1993

School of Electronic Engineering and Computer Science, University of Wales, Dean Street, Bangor, Gwynedd, LL57 1UT, UK. Telephone: +44 248 382691. Fax: +44 248 361429. E-mail: gerry@sees.bangor.ac.uk.

ABSTRACT

1. INTRODUCTION

2. INFORMATION AND REDUNDANCY

   • 2.1 Shannon's Information Theory
   • 2.2 Redundancy as Relatively Frequent Repetition of Patterns
   • 2.3 Algorithmic Information Theory

3. COMPRESSION PRINCIPLES

   • 3.1 Coding for Information Compression
     • 3.1.1 Chunking and Tags
     • 3.1.2 Run-length Coding
     • 3.1.3 Schema Plus Correction
   • 3.2 Finding Redundancy

4. CODING FOR REDUCED REDUNDANCY IN COMPUTING AND COGNITION

   • 4.1 Adaptation and Inhibition in the Nervous System
     • 4.1.1 'Neural' Computing
   • 4.2 Objects and Classes in Perception and Cognition
     • 4.2.1 Seeing the World as Objects
     • 4.2.2 Stereoscopic Vision and Random Dot Stereograms
     • 4.2.3 Classes and Sub-Classes
   • 4.3 Natural Languages
   • 4.4 Grammars
     • 4.4.1 Context-free Phrase Structure Grammars
     • 4.4.2 More Powerful Grammars
   • 4.5 Computer Programs
     • 4.5.1 Functional and Structured Programming
     • 4.5.2 Logic Programming
     • 4.5.3 Object-Oriented Programming
   • 4.6 Other Aspects of Computing

5. SEARCHING FOR REDUNDANCY IN COMPUTING AND COGNITION

   • 5.1 Random Dot Stereograms
   • 5.2 Recognition of Objects and Patterns
   • 5.3 Grammar Discovery, Language Acquisition and Other Kinds of Learning
   • 5.4 Query-by-Example
   • 5.5 De-referencing of Identifiers in Computing
   • 5.6 Memory Access in Computing Systems
   • 5.7 Logical Deduction
     • 5.7.1 Modus Ponens
   • 5.8 Inductive Reasoning and Probabilistic Inference
   • 5.9 Normalisation of Databases
   • 5.10 Parsing

6. CONCLUSION

   • 6.1 The Significance of Information Compression
   • 6.2 Implications
     • 6.2.1 A New Theory of Computing and Cognition
     • 6.2.2 'New Generation' Computing
   • 6.3 Future Work

7. ACKNOWLEDGEMENTS

8. REFERENCES

FIGURE CAPTIONS

ABSTRACT

The article first reviews what is meant by information and, in particular, what is meant by redundancy, a concept which is fundamental in all methods for information compression.

Principles of information compression are described.

The major part of the article describes how these principles may be seen in a range of observations and ideas in computing and cognition: the phenomena of adaptation and inhibition in nervous systems; 'neural' computing; the creation and recognition of 'objects' and 'classes' in perception and cognition; stereoscopic vision and random-dot stereograms; the organisation of natural languages; the organisation of grammars; the organisation of functional, structured, logic and object-oriented computer programs; the application and de-referencing of identifiers in computing; retrieval of information from databases; access and retrieval of information from computer memory; logical deduction and resolution theorem proving; inductive reasoning and probabilistic inference; parsing; normalisation of databases.

1 INTRODUCTION

That brains and nervous systems may be governed by some kind of principle of economy is not a new idea. Although it is currently out of fashion, this notion has attracted intermittent interest from at least as long ago as Zipf's (1949) Human Behaviour and the Principle of Least Effort and Attneave's pioneering ideas (1954) about information processing in visual perception. Other studies in this tradition are referenced at appropriate points below.

That economy may also be a significant feature of computing is less widely recognised. It is prominent, of course, in the literature on data compression and it features in other more or less specialised aspects of computing (some of which will be discussed below). But the intimate connection which appears to exist between information compression and many familiar aspects of computing is not widely understood.

In a previous article, I have developed this idea as a proposed theory of computing (Wolff, 1990), drawing on earlier research on inductive learning (Wolff, 1988). Prototypes have been developed of a 'new generation' computing system which is based on the theory (Wolff & Chipperfield, 1990; Wolff, 1991a - Chapter 5, 1991b, submitted-b). The purpose of this article is to complement the relatively narrow focus of this work with a broader perspective on the several ways in which information compression may be seen in diverse areas of both computing and cognition. The article aims to show how a variety of established ideas may be seen as information compression and to illustrate the broad scope of these principles in information systems of all kinds, both man-made and natural.

The next section reviews what is meant by information and, in particular, what is meant by redundancy, a concept which is fundamental in all methods for information compression. Principles of information compression are then reviewed. The major part of the article is a survey of a range of observations and ideas in computing and cognition which may be understood in terms of information compression.

2 INFORMATION AND REDUNDANCY

The ideas which will be described can be generalized to cases where information takes the form of a continuously varying signal. Analogue cases can be approximated in digital terms with any desired level of precision by varying the granularity of digitisation. The ideas can probably also be generalized to cases where information is distributed in a two-dimensional (or higher dimensional) pattern. But unless I say otherwise, a one-dimensional stream of atomic symbols will be the subject of discussion.

The following three sub-sections describe three distinct views of information and redundancy which appear to complement each other.

2.1 Shannon's Information Theory

If the probabilities of all members of the set of symbol types are equal for every location in a string (eg 0.5 for each of the symbol types 0 and 1) then the information conveyed by the string is a theoretical maximum. In a string like this, the sequence of symbols is random.

If the probabilities of symbol types are not equal at any position in a string then the information conveyed by the string is less than this maximum.The difference between the theoretical maximum and the information contained in a given string is called redundancy. The existence of redundancy in a string of symbols means that the string is not random. Redundancy in information seems to correlate with our subjective impression of 'organisation' or 'structure' in the information.

2.2 Redundancy as Relatively Frequent Repetition of Patterns

The absolute probability of a symbol type can be derived in a straightforward way from the frequency of that symbol type in a reference string. The same is true of contextual probability provided the notion of 'context' can be adequately defined.

One way of dealing with the problem of context is to convert all contextual probabilities into absolute probabilities. This can be done if the notion of a 'symbol type' is generalized from atomic symbols to sequences of atomic symbols. A sequence of atomic symbols may be regarded as a 'composite' symbol type or pattern. In this case, what was previously regarded as the 'context' of a symbol now becomes part of a larger pattern.

Shannon's definition of information says, in effect, that if a given pattern repeats in the reference string more often than the other possible patterns of the same size, then the string contains redundancy. If all the possible patterns of a given size occur equally often then the string is random and contains no redundancy.

There is nothing in what has just been said to imply that the atomic symbols in a pattern are necessarily contiguous or 'coherent'. A sequence of symbols which repeats more often than other sequences of the same size represents redundancy even if the pattern is discontinuous or fragmented and interspersed with other symbols. The significance of this point will be considered at relevant points later.

This view of redundancy - as the relatively frequent repetition of patterns - reflects the everyday meaning of redundancy as something which is 'surplus to requirements'. Information which repeats is information which is unnecessary in terms of its communicative value. Repeated information may, of course, be very useful for such other purposes as error correction or for increasing the speed of responses in computer systems.

2.3 Algorithmic Information Theory

Although randomness and redundancy in AIT seem different from how they appear in Shannon's theory, the two views are probably complementary and not in conflict. Later discussion should help to clarify how they may relate to each other.

3 COMPRESSION PRINCIPLES

The principles which will be described appear to be valid for most of the simpler 'standard' techniques for information compression. With suitable interpretation and analysis, they may also prove to be true of the more elaborate techniques such as linear predictive coding (see, for example, Southcott et al., 1990) or the use of fractals (eg Becker & Dörfler, 1989) or vectors (eg Enderle et al., 1987) for representing graphical information in compressed form. Establishing the scope of the principles is a matter for future research.

The basis of all techniques for information compression is removing some at least of the redundancy from information. Within this frame, two kinds of information compression can be distinguished (Storer, 1988):

• 'Lossless' compression. With this kind of technique, redundant information, and only redundant information, is removed. Since all the non-redundant information is preserved, it is possible in principle and usually in practice to restore the original information with complete fidelity.

• 'Lossy' compression. With lossy compression techniques, redundant information is removed together with some of the non-redundant information. In these cases, the loss of non-redundant information means that the original can never be perfectly restored. This is a penalty which can be and often is outweighed by the benefit of the extra compression which can be achieved and, in many cases, a reduction in the amount of processing needed to achieve compression. For both lossless and lossy compression techniques, two aspects need to be considered:

• How should the compressed information be organised or 'coded'?

• How can redundancy in information be discovered so that it can be removed?

3.1 Coding for Information Compression

Here we can see a link between Shannon's theory and AIT. Information which contains relatively frequent repetition of patterns contains redundancy in Shannon's terms. But the fact of relatively frequent repetition means that the information is compressible - and this in itself means that the information is redundant in terms of AIT.

The idea of reducing redundancy by reducing repetition of patterns comes in three main forms: 'chunking and tags', 'run-length coding' and 'schema plus correction'.

3.1.1 Chunking and Tags

Where a pattern of contiguous symbols is repeated identically in two or more locations within a body of information, these multiple instances may be merged or unified¹ into one single chunk. Merging patterns in this way reduces redundancy but, unless other provision is made, it also loses the non-redundant information about where (all but one of) the patterns were located in the original information.

If this information about locations is to be preserved then it is necessary to give the chunk some kind of name, label or tag and to place an instance of the tag as a 'reference' to the chunk in each of the locations from which the chunk has been removed. Of course, to make a chunk and use tags only makes sense in terms of information saving if the information cost of the tags is less than what is saved by merging patterns.

The connection between the redundancy-removing formation of chunks and the use of tags is not rigid:

• Repeating instances of a pattern may be merged to form a chunk without the use of tags. Compression in this case is lossy because some or all of the information about the locations of the chunk is discarded.

• Tags can sometimes be useful for reasons other than compression when there is only one reference to a tagged object. This can happen with the referencing of books and articles as is discussed briefly later.

There are many variations and refinements of the chunking and tags idea. A well-known refinement is Huffman coding which assigns shorter tags to commonly occurring chunks and longer tags to rare ones (see Storer, 1988, for discussion).

1. The main use of the term unification in this article is to mean a simple merging of multiple instances of any pattern. This idea is related to, but simpler than, the concept of 'unification' in logic which is discussed later in the article.

3.1.2 Run-length Coding

Where a symbol or a pattern of contiguous symbols forms a repeating sequence, the symbol or pattern may be recorded only once, together with something to show how it repeats. For example, a sequence of 1000 ones in binary coded information may be reduced to 1(1000) or 1*. In the first, 'lossless', case the number of repetitions is recorded and the original sequence may be recreated. In the second, 'lossy', case, only the fact of repetition is marked (with '*') and the non-redundant information about the number of repetitions has been discarded.

3.1.3 Schema Plus Correction

Where two or more patterns are similar but not identical, the parts of the patterns which are identical may be recorded as a 'schema' and the parts which are different may be coded as 'corrections' to that schema. A schema like this is a recurrent pattern which may be and often is discontinuous or fragmented in the way which was mentioned earlier.

A 'negation' operator, which is normally seen as a logical primitive, may, in the context of the schema-plus-correction idea, be seen as an aid to compression. If today's shopping list is the same as last week's but with one item omitted, it is more economical for any but the very shortest list to specify today's list as 'last week's, not soap' than to write it out in full.

3.2 Finding Redundancy

For information compression we often want to do more than merely find some redundancy in information - we want to find as much as possible, or, more practically, as much as possible for a reasonable amount of effort. Maximising the amount of redundancy found means maximising R where:

         i=n
     R = SUM (fi - 1) * si
         i=1

Maximising R means searching the space of possible unifications for the set of big, frequent patterns which gives the best value. For a string containing N atomic symbols, the number of possible patterns in which symbol order is preserved (including single atomic symbols and all composite patterns, both coherent and fragmented) is:

P = 2^N - 1

C = P(P - 1) / 2

Since the space is typically so large, the processing costs of searching it with any degree of thoroughness is normally significant and needs to be weighed against the benefits for compression of maximising the amount of redundancy which is found. In this connection, two main tactics are relevant:

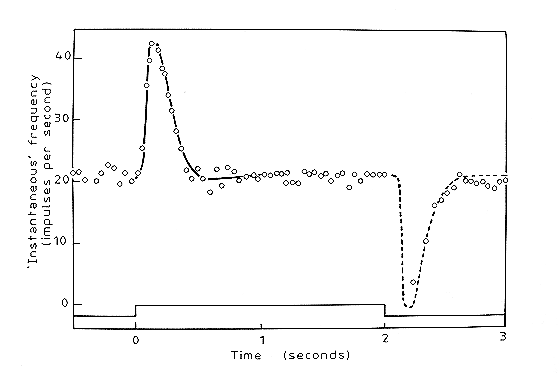
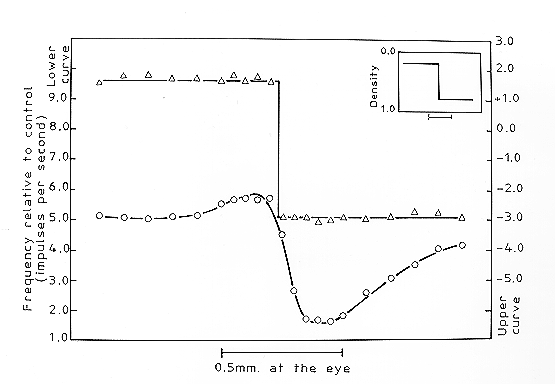
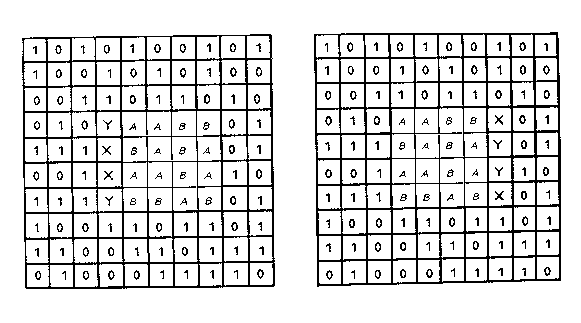
• Restricting the search space. Search costs may be kept within bounds by searching only within a sub-set of the set of possible comparisons. Restrictions of this kind can be seen in most practical techniques for information compression: comparisons may be made only between sub-strings of the same size; or the maximum size of chunks may be restricted; or some other constraint may be imposed.

• Using metrics to guide the search. The costs of searching may be minimised without undue sacrifices in effectiveness by applying a measure of redundancy to guide the search. In search techniques such as 'hill climbing', 'beam search', 'best-first search', 'branch-and- bound search' the search effort is curtailed in those parts of the search space which have proved sterile and it is concentrated in areas which are indicated by the metric.

4 CODING FOR REDUCED REDUNDANCY IN COMPUTING AND COGNITION

4.1 Adaptation and Inhibition in the Nervous System

This kind of adaptation at the level of our conscious awareness can be seen also at a much lower level in the way individual nerve cells respond to stimulation. The two studies to be described are of nerve cells in a horseshoe crab (Limulus) but the kinds of effects which have been observed in this creature have also been observed in single neurone studies of mammals and appear to be widespread amongst many kinds of animal, including humans. There are more complex modes of responding but their existence does not invalidate the general proposition that nervous tissue is relatively sensitive to changes in stimulation and is relatively insensitive to constant stimulation.

Figure 1 shows how the rate of firing of a single receptor (ommatidium) in the eye of Limulus changes with the onset and offset of a light (Ratliff, Hartline & Miller, 1963). The receptor responds with a burst of spike potentials when the light is first switched on. Although the light stays bright for some time, the rate of firing quickly settles down to a background rate. When the light is switched off, there is a brief dip in the rate of firing followed by a resumption of the background rate.

Figure 1. Variation in the rate of firing of a single ommatidium of Limulus in response to changing levels of illumination (Ratliff, Hartline & Miller, 1963, p 118).

This relative sensitivity to changes in stimulation and relative insensitivity to constant stimulation can be seen also in the spatial dimension. Figure 2 shows two sets of recordings from a single ommatidium of Limulus (Ratliff & Hartline, 1959). In both sets of recordings, the eye of the crab was illuminated in a rectangular area bordered by a dark rectangle of the same size. In both cases, successive recordings were taken with the pair of rectangles in successive positions across the eye along a line which is at right angles to the boundary between light and bright areas. This achieves the same effect as - but is easier to implement than - keeping the two rectangles in one position and taking recordings from a range of receptors across the bright and dark areas.

Figure 2. Two sets of recordings from a single ommatidium of Limulus (Ratliff & Hartline, 1959, p 1248).

In the top set of recordings (triangles) all the ommatidia except the one from which recordings were being taken were masked from receiving any light. In this case, the target receptor responds with frequent impulses when the light is bright and at a sharply lower rate when the light is dark.

In the bottom set of recordings (circles) the mask was removed so that all the ommatidia were exposed to the pattern of bright and dark rectangles. In this situation, the target receptor fires at or near a background rate in areas which are evenly illuminated (either bright or dark) but, near the border between bright and dark areas, positive and negative responses are exaggerated. In the spatial dimension, as with the temporal dimension, changes in stimulation are more significant than constant stimulation.

It is now widely recognised that this sensitivity to temporal and spatial discontinuities in stimulation is due to the action of inhibitory pathways in the nervous system which counteract the excitation of nerve cells. The way inhibition may explain the observations which have just been described and a range of other phenomena (Mach bands, simultaneous contrast, motion sensitivity) is well described and discussed by Von Békésy (1967).

It has also been recognised for some time that these phenomena may be understood in terms of principles of economy in neural functioning (see, for example, Barlow, 1969). In the terms discussed earlier, adaptation and inhibition in nervous functioning have an effect which is similar to that of the run-length coding technique for data compression. Economy is achieved in all these cases by coding changes in information and reducing or eliminating the redundancy represented by sequences or areas which are uniform (Von Békésy, 1967).

4.1.1 'Neural' Computing

The idea that principles of economy may apply to neural functioning is recognised in some of the theory associated with artificial 'neural' computing, eg 'Hopfield nets' (Hopfield, 1982) and 'simulated annealing' (Hinton & Sejnowski, 1986). But with some notable exceptions (eg Mahowald & Mead, 1991), there seems to have been little attempt in the development of artificial neural networks to exploit the kinds of mechanisms which real nervous systems apparently use to achieve information compression.

4.2 Objects and Classes in Perception and Cognition

4.2.1 Seeing the World as Objects

Some things in our everyday experiences are so familiar that we often do not realise how remarkable they are. One of these is the automatic and unconscious way we see the world as composed of discrete objects. Imagine a film taken with a fixed camera of a tennis ball crossing the field of view. Successive frames show the ball in a sequence of positions across a constant background. Taken together, these frames contain a very large proportion of redundancy: the background repeats in every frame (apart from that part of the background which is hidden behind the ball) and the ball repeats in every frame (let's assume that it is not spinning). Uniform areas within each frame also represent redundancy.

Any simple record of this information - on cinema film or digitised images - is insensitive to the redundancy between frames or within frames and has no concept of 'ball' or 'background'. But people automatically collapse the several images of the ball into one coherent concept and, likewise, see the background as the 'same' throughout the sequence of frames.

This is a remarkable piece of information compression, especially since it is performed in real time by nerve cells which, by electronic standards, are exceedingly slow. On this last point, Mahowald & Mead's work, referenced above, throws useful light on how this kind of compression may be achieved in a simulated mammalian retina and how the necessary speed can be achieved with slow components. In keeping with what was said earlier about neural functioning, inhibitory pathways and processes are significant.

Of course, the concepts we have of real-world objects are normally more complicated than this example suggests. The appearance of a typical object varies significantly depending on orientation or view point. In cases like this, each concept which we form must accommodate several distinct but related views. What we normally think of as a unitary entity should, perhaps, be regarded more accurately as a class of inter-related snapshots or views (more about classes below).

Notwithstanding these complexities, our everyday notion of an object is similar to the previously-described concept of a chunk. Like chunks, objects often have names or tags but again, as with chunks, not every object has a name. An object (with or without a name) may, like a chunk, be seen as the product of processes for extracting redundancy from information.

4.2.2 Stereoscopic Vision and Random Dot Stereograms

"In an animal in which the visual fields of the two eyes overlap extensively, as in the cat, monkey, and man, one obvious type of redundancy in the messages reaching the brain is the very nearly exact reduplication of one eye's message by the other eye." (Barlow, 1969, p 213).

Stereoscopic vision and the phenomenon of random dot stereograms provides further evidence of information compression by our nervous systems. It also provides a striking illustration of the connection between redundancy extraction and our tendency to see the world as discrete objects.

Each of the two images in Figure 3 is a random pattern of black and white pixels. Each image, in itself, contains little or no redundancy. But when the two images are taken together, there is substantial redundancy because they have been designed so that they are almost, but not quite, the same. The difference is that a square area in the left image has been shifted a few pixels to the right compared with a corresponding square area in the right image, as is illustrated in Figure 4.

Figure 3. A random-dot stereogram (from Julesz, 1971, p 21).

Figure 4. Diagram to show the relationship between the left and right images in Figure 3 (based on Julesz, 1971, p 21).

When the images are viewed through a stereoscope - so that the left image is seen by the left eye and the right image by the right eye - one's brain fuses the two images so that the two areas around the squares are seen as the 'same' and the two square areas are merged into a single square object which appears to stand out vividly in front of its background.

Random dot stereograms like this are normally used to illustrate and study human abilities to perceive depth using stereoscopic vision. But they are also good examples of our ability to extract redundancy from information by merging matching patterns.

In Figure 3, the central square, and its background, are chunks in the sense described earlier, each of which owes its perceptual existence to the merging of matching patterns. It is the redundancy which exists between the two images, coupled with our ability to find it, which gives coherence to the objects which we see. The vivid boundary which we can see between the square and its background is the product of search processes which successfully find the maximum possible unification between the two images.

In everyday vision (eg the tennis ball example discussed above) recognition of an object may owe something to redundancy within each frame. Since each of the two images in a random dot stereogram contains little or no redundancy, our ability to see coherent objects in such stereograms demonstrates that we do not depend on redundancy within each image but can derive an object concept exclusively from redundancy between images.

4.2.3 Classes and Sub-Classes

It is commonly recognised that objects may be grouped into classes and classes may themselves be grouped into higher level classes. Cross-classification with overlapping classes (eg 'woman' and 'doctor') is also seen.

A class may be defined extensionally by listing its constituent objects or classes. It may also be defined intensionally in terms of attributes which members of the class have in common. Although many commonly-used classes are 'polythetic' - no single attribute need necessarily be shared by all members of the class - it is similarity amongst members of a class - some degree of sharing of attributes - which gives 'natural' classes their coherence.

Grouping things by their similarity gives us a means of compressing the information which describes them. An attribute which is shared by all members of a class (or, in the case of polythesis, a set of alternative attributes which is shared by members of a class) need be recorded only once and not repeated for every member. The shared attributes of a class constitute a 'schema' in the sense discussed earlier, which may be 'corrected' for each member by the addition of more specific information about that member.

The widespread use of classes and subclasses in our thinking and in language, coupled with their obvious value in compressing information, strongly suggests that we do store classes and attributes in this way. But it is difficult to obtain direct confirmation of this idea. Attempts to verify the idea experimentally (eg Collins & Quillian, 1972) have proved inconclusive. This is probably more to do with the difficulties of making valid inferences from experimental studies of human cognition than any intrinsic defect in the idea.

4.3 Natural Languages

Without a convenient brief label like 'table', the concept of a 'horizontal platform with four, sometimes three, vertical supports, normally about three feet high, normally used for ...' would have to be long-windedly repeated in every relevant context rather like the slow language of the Ents in Tolkien's The Lord of the Rings. A sentence is normally a highly 'coded' and compressed representation of its meanings.

An even more obvious example of tags in natural language is the use of 'references' in books or articles. "(Zipf, 1949)" is an example which appears in the second paragraph of this article and also in the paragraph after this; it references the fuller details given at the end of the article. These details may themselves be seen as a label for the whole book. Like any tag, a reference can circumvent the need to repeat information redundantly in two or more contexts. But it can be and often is convenient to use this device for reasons of consistency and style when a given reference appears only once in a book or article.

Before leaving this section on natural language, it is relevant to comment on Zipf's extensive studies of the distribution of words in natural languages (Zipf, 1935) and his Principle of Least Effort (Zipf, 1949), mentioned earlier, which he proposed to explain these observations and others. Zipf's arguments are interesting and quite persuasive but, as Mandelbrot (1957) and others have pointed out, the phenomena described by 'Zipf's law' could be due to nothing more profound than a random process for creating words and the boundaries between words in natural languages. However, in George Miller's words (1965), "It is impossible to believe that nothing more is at work to guide our choice of letter sequences than whatever random processes might control a monkey's choice, or that the highly plausible arguments Zipf puts forward have not relevance at all." (p vii). The jury is still out!

4.4 Grammars

4.4.1 Context-free Phrase Structure Grammars

Compression is illustrated by the grammar shown in Figure 5. This grammar is written according to the notational conventions of context-free phrase structure grammar (CF-PSG), a simple type of grammar which is essentially the same as Backus Normal Form (BNF), commonly used to represent the syntax of computer languages.

S -> NP V NP
NP -> D N
D -> the
D -> a
N -> boy
N -> girl
V -> likes
V -> meets

Figure 5. A context-free phrase structure grammar.

This grammar represents the set of terminal strings (sentences) which include the boy meets the girl, the girl likes the boy etc but with none of the redundancy represented by repeated instances of individual words - boy, girl etc - or of 'noun phrase' groupings like the boy, the girl etc. These repeating elements are 'chunks' of information in the sense described earlier. The symbols S, NP, V, D and N are 'tags' used to identify their corresponding chunks in each of the contexts in which they occur.

Notice that a grammar like the one just shown says nothing about the order in which the sentences may appear and it says nothing about how many of each sentence may appear. A grammar is typically a 'lossy' compression of any one sample of the language which it represents.

The 'chunks with tags' device also permits the encoding of recursion which can itself be seen as a form of run-length coding. The fragment of grammar shown in Figure 6 generates phrases like the very very very tall girl, a very very short boy etc. Notice that the number of instances of very in any one phrase is not specified: recursion like this represents lossy compression of any finite set of terminal strings.

NP -> D V A N
D -> the
D -> a
V -> NULL
V -> very V
A -> tall
A -> short
N -> boy
N -> girl

Figure 6. A CF-PSG with recursion.

4.4.2 More Powerful Grammars

It has been recognised for some time (and pointed out most notably by Chomsky, 1957) that CF-PSGs are not 'powerful' enough to represent the structure of natural languages effectively. As shown by the examples just given, CF-PSGs can be used to represent simple sub-sets of English in a succinct form. But the full complexity of English or other natural language can only be accommodated by a CF-PSG, if at all, at the cost of large amounts of redundancy in the grammatical description.

The phenomenon of 'discontinuous dependencies' highlights the shortcomings of CF- PSGs. In a sentence like The winds from the West are strong, there is a 'number' dependency between winds and are: the plural noun must be followed by a plural verb and likewise for singulars. The dependency is 'discontinuous' because it jumps over the intervening structure (from the West in the example) and this intervening structure can be arbitrarily large.

To represent this kind of dependency with a CF-PSG requires one set of rules for singular sentences and another set of rules for plurals - and the two sets of rules are very similar. The consequent redundancy in the grammar can multiply substantially when other dependencies of this kind are included.

This problem can be largely overcome by using a more 'powerful' kind of grammatical system like a Definite Clause Grammar (Pereira & Warren, 1980) or a Transformational Grammar (see, for example, Radford, 1988). This kind of system may be seen as a superset of a CF-PSG with additional mechanisms which, amongst other things, allow discontinuous dependencies to be represented without undue redundancy.

It is not appropriate here to discuss these systems in detail. In general, they can be seen as variations on the 'schema-plus-correction' idea which was described above. They provide the means of representing sentence structure as a 'schema' which may, in the example given earlier, be 'corrected' by the addition of singular or plural components at appropriate points in the structure.

4.5 Computer Programs

Elsewhere (Wolff, submitted-a) I have discussed how a computer program or mathematical function may be seen as a compressed representation of its inputs and its outputs, how the process of designing programs and functions may be seen to be largely a process of information compression, and how the execution of programs or functions may also be seen in terms of information compression.

In this section, I view computer programs more conventionally as a set of 'operations' and discuss how principles of compression may be seen in the way programs are organised. In the the same way that the notational conventions used in grammars may be regarded as a means of compressing linguistic information, the conventions used in computer programs may be seen as devices for representing computing operations in a succinct form. As with grammars, the provision of these facilities does not in itself guarantee that they will be used to best effect.

Compression techniques may be seen in 'functional', 'structured' and 'logic' programming and, a fortiori in 'object-oriented' programming.

4.5.1 Functional and Structured Programming

Chunking and tags. If a set of statements is repeated in two or more parts of a program then it is natural to declare them once as a 'function', 'procedure' or 'sub-routine' within the program and to replace each sequence with a 'call' to the function from each part of the program where the sequence occurred. This is an example of compression: the function may be regarded as a 'chunk' and the name of the function is its 'tag'.

Whether or not a programmer chooses to create a function in a situation like this - or to leave repeated sequences as 'macros' - depends, amongst other things, on whether the sequence is big enough to justify the 'cost' of giving it a name and whether the run-time overhead which is typically associated with the use of functions in conventional computers is acceptable for the application in hand.

Run-length coding. If a body of code is repeated in one location within the program then it may be declared as a function or marked as a 'block' and the fact of repetition may be marked with one of the familiar conventions for showing iteration: repeat ... until, while ... do, for ... do. Each of these is a form of run-length coding.

Recursion, which is available in most procedural programming languages, is another means of showing repetition of program operations. It is essentially the same as recursion in grammars.

Schema plus correction. It often happens in software design that two or more sets of statements are similar but not identical. In these cases, it is natural to merge the parts which are the same and to provide conditional statements (if ... then ... else statements or case statements) to select alternative 'paths' within the software. The complete set of statements, including the conditional statements, may be regarded as a 'schema' describing a set of behaviours for the program, much as a grammar describes a set of terminal strings.

To specify a particular path through the program, it is necessary to supply the information needed in the conditional statements so that all the relevant choices can be made. This additional information is the 'correction' to the schema represented by the program code. If the program statements have been encapsulated in a function then these corrections to the program schema will normally be supplied as arguments or parameters to the function.

4.5.2 Logic Programming

Similar ideas appear in logic programming languages like Prolog. For example, the chunking and tags idea can be seen in the structure of a Prolog Horn clause. The predicate in the head of the clause may be seen as a label or tag while the body of the clause may be seen as the chunk which it labels.

As with functional and structured programs, a Prolog program may be seen as a schema which represents the set of possible behaviours of the program. The information supplied in a Prolog query serves as a correction to the schema which reduces the range of possible behaviours of the program.

Repetition in Prolog programs is coded using recursion. 4.5.3 Object-Oriented Programming Object-oriented programming (OOP), as it was originated in Simula and has been developed in Smalltalk, C++ and several other languages, embraces the kinds of mechanisms just described but includes an additional set of ideas which may also be understood in terms of information compression.

One important idea in OOP, which was introduced in Simula, is that there should be a one- for-one correspondence between objects in the real world and 'objects' in the software. For example, an OO program for managing a warehouse will have a software object for every person employed in the warehouse, a software object for every shelf or bay, a software object for every item stored, and so on. In OO terms, a software object is a discrete piece of program: data structures and associated procedural code or either of these without the other. For example, an object for a 'person' would be a program which can respond to 'messages' such as a request for the person's name, an instruction to move an item from one location to another, and so on.

Superficially, this is an extravagant - and redundant - way to design software because it seems to mean that the same code is repeated in every object of a given type. But, of course, this is not how things are done. As with 'real world' objects, economy can be achieved by the use of classes and sub-classes.

In OO programming languages, every object belongs to a class (in some OO languages an object can be assigned to more than one class), the code for that class is stored only once within the program and is inherited by each instance of the class. There can be a hierarchy of classes with inheritance of code from any level down to individual objects.

As with individual objects, a recognised principle of OOP is that the classes which are defined in an OO program should correspond, one for one, with the classes which we recognise in the real world. In the warehouse example, there would be a class for each of 'person', 'shelf' and 'item'. Each class - 'person', for example - may be divided into sub-classes like 'manager', 'foreman', 'operative' etc.

The ideas which have been described - software objects, classes and inheritance - are further examples of the way information compression pervades the organization of computer programs:

• As discussed earlier, objects and classes as we see them in the real world may be understood in terms of our subjective compression of perceptual information received from the world. By using similar devices in software design we can make the structure of software reflect patterns of redundancy in the real world which our brains are apparently so efficient at exploiting.

• Within the program code itself, class hierarchies with inheritance of code are powerful mechanisms for information compression. Instances of a class may be multiplied without creating any corresponding redundancy because all the data structures and procedural code which they have in common can be inherited from the class definition. Likewise, sets of classes which have common attributes may inherit these attributes from a higher level class.

• As was mentioned in connection with natural classes, the mechanisms of class hierarchies with inheritance may be seen as an example of the schema plus correction technique for information compression: a class definition is a 'schema' and information which is supplied when a new instance of the class is created (eg the name of that object) is a 'correction' to the schema. In a similar way, a high level class may be seen as a relatively abstract schema which is refined or 'corrected' by the more specific information contained in lower level classes.

  It is perhaps pertinent to comment, in passing, on the advantages of designing software in this way:

• One advantage is psychological: software which reflects the structure of our established concepts is easier to understand than software which does not.

• A more subtle, but nonetheless important, advantage is that software designed in this way will normally be easier to modify than otherwise: the fact that the structures reflected in the software are persistent (repeating) patterns in the world means that new versions of software are more likely to be refinements or rearrangements of already established objects and classes than radical reorganizations of the code.

• There is a third advantage for software designers in using these mechanisms for information compression: if any given piece of information is recorded only once within a program then any change to that information needs be made only once and there is no need to check that it is correctly repeated in other parts of the program

4.6 Other Aspects of Computing

• Names of tables or records in databases.

• Names of fields in tuples or records.

• Names of files.

• Names of variables, arrays and other data structures used in computer programs.

• Labels for program statements (for use with the now shunned 'go to' statements).

The names of directories in Unix, MS-DOS and similar operating systems are also tags in the sense of this article. But an hierarchical directory structure may also be seen as a simple form of class hierarchy and, as such, it may be seen as a restricted form of schema plus correction. The name of a directory is a name which applies to all the files and sub-directories within that directory and to all files and sub-directories at lower levels. Rather than redundantly repeat the name for every file and sub-directory to which it applies, the name is recorded once and, in effect, 'inherited' by all the objects at lower levels.

5 SEARCHING FOR REDUNDANCY IN COMPUTING AND COGNITION

As we have seen, searching for redundancy can be understood as a search for patterns which match each other and, as we have seen, there is normally a need to circumscribe the search or to guide the search by some measure of redundancy or both. The sections which follow describe some of the ways in which this kind of search appears in computing and cognition. As with the section on coding, earlier examples are mainly from natural information processing with later examples from computing.

5.1 Random Dot Stereograms

In this case, assuming the left image has the same number of pixels as the right image, the size of the search space is P² where P is the number of possible patterns in each image, calculated in the same way as before. (The fact that the images are two dimensional needs no special provision because the original formula covers all combinations of atomic symbols.)

For any stereogram with a realistic number of pixels, this space is very large. Even with the very large processing power represented by the 10¹⁰ neurones in the brain, it is inconceivable that this space can be searched in a few seconds and to such good effect without the use of metrics- guided searching of the kind described earlier and probably also with some restriction on what comparisons between patterns will be made.

David Marr (1982, Chapter 3) describes two algorithms which solve this problem. In line with what has just been said, both algorithms rely on constraints on the search space and both may be seen as incremental search guided by redundancy-related metrics.

5.2 Recognition of Objects and Patterns

How we recognise objects and other patterns is, of course, the subject of much research and is certainly not yet well understood. Amongst the complexities of the subject is the problem, mentioned earlier, of how we can recognise objects despite variations in their appearance due to variations in orientation. Likewise, we can recognise patterns such as handwriting despite many variations of style.

Despite these complexities, it is reasonably clear that, in general terms, the phenomenon of recognition can be understood as information compression. Recognition of an object or a pattern means the partial or complete unification of perceptual input with a corresponding pattern already in memory - and thus an overall reduction in the information which they jointly contain.

5.3 Grammar Discovery, Language Acquisition and Other Kinds of Learning

In line with these expectations, practical techniques for grammar discovery are largely a search for repeating patterns in data with unification of repeating patterns, the assignment of tags and, quite often, a discard of some portion of the non-redundant information in the samples (Wolff, 1982, 1987). Principles of economy have been recognised in this field for some years (Cook & Rosenfeld, 1976).

The learning of a first language by children is clearly a richer and more complex process than grammar discovery as it is normally understood. But computer models of language learning which I have developed in earlier research, which are based on principles of information compression, show remarkable correspondences in their learning behaviour to well-documented phenomena in the way children learn a first language (Wolff, 1988):

• The unsupervised induction of grammatical structure, including segmental structure (words and phrases) and disjunctive structure (parts of speech and other classes).

• Generalisation of rules and correction of overgeneralisations without external error correction.

• The way the rate of acquisition of words and other structures varies as learning proceeds.

• The order in which words are acquired.

• Brown's (1973) Law of Cumulative Complexity.

• The S-P/episodic-semantic shift.

• The learning of semantic structures and their integration with syntax.

• The word frequency effect.

This evidence lends support to the proposition that language learning may be understood, in large measure, as information compression.

Other kinds of learning have also been analysed in terms of economical coding. Pioneering work on the learning of classifications (Wallace & Boulton, 1968) has been followed by related work on economical description of data (eg Wallace & Freeman, 1987; Rissanen, 1987; Cheeseman, 1990; Pednault, 1991; Forsyth, 1992). A significant strand of thinking in much of this work is the close connection between compact coding and probabilistic inference.

5.4 Query-by-Example

A commonly-used technique for retrieving records from a database is to provide a query in the form of an incomplete record - an 'example' of the kind of complete record which is to be retrieved. This is illustrated in Figure 7 where the query 'example' has the general form of the complete records but contains asterisks ('*') where information is missing. The search mechanisms in the database match the query with records in the database to retrieve the zero or more records which fit.

An 'example' used as a query:

Name: John *
Address: * New Street *

Some records in a database:

Name: Susan Smith
Address: 8 New Street, Chicago
Name: John Jones
Address: 4 New Street, Edinburgh
Name: John Black
Address: 20 Long Street, London
Name: David Baker
Address: 41 Avenue des Pins, Paris
...

Figure 7. A query and database records to illustrate query-by-example.

Most systems of this kind are driven by some kind of redundancy-related metric. In Figure 7, there is some degree of matching between the query and the first three of the records shown. But John Jones of 4 New Street, Edinburgh is the preferred choice because it gives a better fit than the other records.

Retrieval of a record may be seen as 'unification' between the record and the query and a corresponding extraction of the redundancy between them. However, this compression is normally evanescent, appearing only temporarily on the operator's screen. When a query operation has been completed, the records in the database are normally preserved in their original form, while the unification and the query are normally deleted from the system.

5.5 De-referencing of Identifiers in Computing

Finding an object by means of its name - 'de-referencing' the identifier - means searching for a match between the 'reference' as it appears without its associated object (eg a 'call' to a program function) and the same pattern as it appears attached to the object which it identifies (eg a function name together with the function declaration).

Finding an object by means of its name is like a simple form of query-by-example. The name by itself is the incomplete record which constitutes the query, while the object to be found, together with its name, corresponds to the complete record which is to be retrieved.

As with query-by-example, there is normally some kind of redundancy-related metric applied to the search. In conventional computing systems, a 'full' match (including the termination marker) is accepted while all partial matches are rejected. A character-by-character search algorithm may be seen as a simple form of hill-climbing search. The seemingly 'direct' technique of hash coding exploits memory access mechanisms which, as is described below, may also be understood in terms of metrics-guided search.

As with query-by-example, unification and compression are less obvious than pattern matching and search. Certainly, a computer program is not normally modified by de-referencing of the identifiers it contains. Unification and compression are confined to the evanescent data structures created in the course of program execution.

5.6 Memory Access in Computing Systems

Information contained in a computer memory - 'data' or statements of a program - can be accessed by sending an 'address' from the CPU to the computer memory along an address bus. The address is a bit pattern which is 'decoded' by logic circuits in the computer memory. These have the effect of directing the pattern to the part of the memory where the required information is stored.

The logic circuits in memory which are used to decode a bit pattern of this kind have the effect of labelling the several parts of memory with their individual addresses. Accessing a part of memory by means of its address may be seen as a process of finding a match between the access pattern and the address as it is represented in computer memory - together with a unification of the two patterns. The search process is driven by a metric which leads to a full match via successively improving partial matches.

5.7 Logical Deduction

Unification in this sense embraces the simpler sense of the word as it has been used in this article. A significant part of logical deduction as it appears in systems like Prolog is the comparison or matching of patterns and their effective merging or unification to make one. The wide scope of unification in the sense of logic is recognised in a useful review by Knight (1989).

As was the case in query-by-example, de-referencing of identifiers and memory access, systems for resolution theorem proving normally look for a full match between patterns and reject all partial matches. This feature - and the search techniques which are normally used to find matching patterns - may be seen as a crude but effective application of metrics to pattern matching and unification.

5.7.1 Modus Ponens

Similar ideas may be seen in more traditional treatments of logic (eg Copi, 1986). Consider, for example, the modus ponens form of logical deduction which may be represented in abstract logical notation like this:

1 p IMPLIES q
2 p
3 THEREFORE q

1 If today is Tuesday then tomorrow will be Wednesday.
2 Today is Tuesday.
3 Therefore, tomorrow will be Wednesday.

The implication p IMPLIES q (today being Tuesday implies that tomorrow will be Wednesday) may be seen as a 'pattern', much like a record in a database.

The proposition p ('today is Tuesday') may be seen as an incomplete pattern, rather like the kind of database query which was discussed earlier. Logical deduction may be seen as a unification of the incomplete pattern, p, with the larger pattern, p IMPLIES q, with a consequent 'marking' of the conclusion, q ('tomorrow will be Wednesday').

Of course, there is a lot more to be said about logic than this. Elsewhere (Wolff, 1991a, Chapter 5; 1991b), I have discussed some of the associated issues including notions of 'true' and 'false', 'negation', and the 'chaining' of logical deductions.

(Editor's note: The logical symbols representing IMPLIES and THEREFORE could not be displayed in the HTML version but are present in the original postscript document)

5.8 Inductive Reasoning and Probabilistic Inference

A popular example of inductive reasoning is the way (in low latitudes) we expect the sun to rise in the morning because it has always done so in our experience in the past. Past experience, together with the proposition that it is night time now, are the 'premises' which lead us to conclude that the sun is very likely to rise within a few hours. Our expectation is strong but there is always a possibility that we may be proved wrong.

There are countless examples like this where our expectations are governed by experience. We expect buds to 'spring' every Spring and leaves to 'fall' every Fall. We expect fire where we see smoke. We expect water to freeze at low temperatures. And we expect to be broke after Christmas!

The way we mentally merge the repeating instances of each pattern in our experience may be seen as further evidence of chunking in human cognition and, as such, further evidence of how human cognition is geared to the extraction of redundancy from information.

Like query-by-example, de-referencing of identifiers, memory access and logical deduction, inductive reasoning may be seen as the matching and unification of a pattern with a larger pattern of which it is a part. Our experience of day following night is a sequential pattern: (night sunrise). The observation that it is night time now is another pattern: (night). The second pattern will unify with the first part of the first pattern and, in effect, 'mark' the remainder of that pattern as an expectation or conclusion.

As was noted earlier, there is a significant body of work on economical description and its connection with probabilistic inference. The connection between these two topics and the topics of pattern matching and unification seems, not yet, to be properly recognised. 5.8.1 The Possible Integration of Deductive and Inductive Reasoning That deductive and inductive reasoning may both be seen as the matching and unification of a pattern with a larger pattern which contains it suggests that they are not as distinct as has traditionally been thought. The example of modus ponens reasoning given earlier may be seen as inductive reasoning: the way Wednesday always follows Tuesday is a (frequently repeated) pattern in our experience and the observation that today is Tuesday leads to an inductive expectation that tomorrow will be Wednesday.

The possible integration of deductive and inductive reasoning is discussed more fully in Wolff (1991b) and Wolff (submitted-b).

5.9 Normalisation of Databases

If, for example, a database contains tables for 'buildings' and for 'sites' both containing columns such as 'location', 'value', 'date-acquired', 'date-of-disposal', then these columns (perhaps with others) may be extracted and placed in a table for 'property'. With suitable provision for linkage between tables, this information may be 'inherited' by the tables for 'buildings' and 'sites' (and other sub-classes of property), much in the manner of object-oriented design.

5.10 Parsing

That parsing must be guided by some kind of redundancy-related metric is most apparent with the ambiguous grammars and relatively sophisticated parsers associated with natural language processing (see, for example, Spärk Jones & Wilkes, 1985). In these cases, alternative analyses may be graded according to how well the grammar fits the text. But even with the supposedly unambiguous grammars and simple parsing techniques associated with computer languages, there is an implicit metric in the distinction between a 'successful' full parse of the text and all failed alternatives - much like the all-or-nothing way in which identifiers are normally recognised in computing.

6 CONCLUSION

6.1 The Significance of Information Compression

Other considerations suggest that information compression is much more significant than that:

• We gather information and store it in brains and computers because we expect it to be useful to us in the future. Natural and artificial information processing is founded on the inductive reasoning principle that the past is a guide to the future.

• But stored information is only useful if new information can be related to it. To make use of stored patterns of information it must be possible to recognize these patterns in new information. Recognition means matching stored patterns with new information and unification of patterns which are the same. And this means information compression in the ways that have been discussed.

• The inductive principle that the past is a guide to the future may be stated more precisely as the expectation that patterns which have occurred relatively frequently in the past will tend to recur in the future. But 'relatively frequent repetition of patterns' means redundancy! It is only possible to see a pattern as having repeated relatively frequently in the past by the implicit unification of its several instances - and this means extraction of redundancy and compression of information in the ways that have been discussed.

These arguments point to the conclusion that information compression is not an incidental feature of information systems. It is intimately related to the principle of inductive reasoning which itself provides a foundation or raison d'être for all kinds of system for the storage and processing information.

6.2 Implications

The prototype systems which we have developed, which are described in the publications just referenced, demonstrate how logical deduction, probabilistic inference, inductive learning, information retrieval and other capabilities may be derived from information compression.

Evidence to date suggests that, when it is fully developed, the SP system will provide many benefits and advantages compared with conventional computers in the storage and retrieval of knowledge, in software engineering and in artificial intelligence (Wolff, 1991a, Chapter 6).

6.3 Future Work

• Developing the SP system and running it on varied examples provides a forcing ground for the theory and its applications.

• In parallel with this work we are studying a range of established concepts in computing, cognition and related fields like mathematics and linguistics to see whether and how they may be interpreted in terms of information compression.

This area of research promises to be a very fruitful field of investigation. Contributions by other researchers will be very welcome.

7 ACKNOWLEDGEMENTS

The work reported in this article was supported in part by a grant from the UK Science and Engineering Research Council (GR/G51565).

8 REFERENCES

Barlow H B (1969). Trigger features, adaptation and economy of impulses. In K N Leibovic (Ed), Information Processing in the Nervous System. New York: Springer, pp 209-230.

Becker K-H & Dörfler M (1989). Dynamical Systems and Fractals, Cambridge: Cambridge University Press.

Brown R (1973). A First Language: The Early Stages. Harmondsworth: Penguin.

Chaitin G J (1987). Algorithmic Information Theory. Cambridge: Cambridge University Press.

Chaitin G J (1988). Randomness in arithmetic. Scientific American 259(1), 80-85.

Cheeseman P (1990). On finding the most probable model. In J Shrager and P Langley (Eds), Computational Models of Scientific Discovery and Theory Formation. San Mateo, Ca.: Morgan Kaufmann.

Chomsky N (1957). Syntactic Structures, The Hague: Mouton.

Collins A M & Quillian M R (1972). Experiments on semantic memory and language comprehension. In L W Gregg (Ed), Cognition in learning and memory. New York: Wiley, pp 117-147.

Copi I M (1986). Introduction to Logic. London: Macmillan.

Cook C M& Rosenfeld A (1976). Some experiments in grammatical inference. In J C Simon (Ed), Computer Oriented Learning Processes, Leyden: Noordhoff, pp 157-174.

Date C J (1986). An Introduction to Database Systems, Vol I, Reading, Mass: Addison-Wesley.

Enderle G, Kansy K & Pfaff G (1987). Computer Graphics Programming, Berlin: Springer- Verlag.

Forsyth R S (1992). Ockham's Razor as a gardening tool: simplifying discrimination trees by entropy min-max. In M A Bramer and R W Milne (Eds), Research and Development in Expert Systems IX, Cambridge: Cambridge University Press, pp 183-195.

Held G & Marshall T R (1987). Data Compression: Techniques and Applications, Hardware and Software Considerations, Second Edition, Chichester: Wiley.

Hinton G E & Sejnowski T J (1986). Learning and relearning in Boltzmann machines. In D E Rumelhart and J L McClelland (Eds), Parallel Distributed Processing, Vol I, Cambridge Mass: MIT Press, pp 282-317.

Hopfield J J (1982). Neural networks and physical systems with emergent collective properties. Proceedings of the National Academy of Science, USA 79, 2554-2558.

Julesz B (1971). Foundations of Cyclopean Perception, Chicago: Chicago University Press.

Knight K (1989). Unification: a multidisciplinary survey. ACM Computing Surveys 21(1), 93-123.

Mahowald M A & Mead C (1991). The silicon retina. Scientific American 264(5), 40-47.

Mandelbrot B (1957). Linguistique Statistique Macroscopique. In L Apostel, B Mandelbrot and A Morf, Logique, Langage et Theorie de l'Information, Paris: Presses Universitaires de France, pp 1-78.

Marr D (1982). Vision: a Computational Investigation into the Human Representation and Processing of Visual Information. San Francisco: Freeman.

Miller G A (1965). Introduction. In Zipf (1935).

Miller G A & Friedman E A (1958). The reconstruction of mutilated English texts. Information & Control 1, 38-55.

Pednault E P D (1991). Minimal length encoding and inductive inference. In G Piatetsky-Shapiro and W J Frawley (Eds), Knowledge Discovery in Databases, Cambridge Mass.: MIT Press.

Pereira F C N & Warren D H D (1980). Definite clause grammars for language analysis - a survey of the formalism and a comparison with augmented transition networks. Artificial Intelligence 13, 231-278.

Radford R (1988). Transformational Grammar: a First Course, Cambridge: Cambridge University Press.

Ratliff F & Hartline H K (1959). The response of Limulus optic nerve fibres to patterns of illumination on the receptor mosaic. Journal of General Physiology 42, 1295-1300.

Ratliff F, Hartline H K & Miller W H (1963). Spatial and temporal aspects of retinal inhibitory interaction. Journal of the Optical Society of America 53, 110-120.

Rissanen J (1987). Stochastic complexity. Journal of the Royal Statistical Society B 49(3), 223- 239.

Robinson J A (1965). A machine-oriented logic based on the resolution principle. Journal of the Association for Computing Machinery 12(1), 23-41.

Shannon C E & Weaver W (1949). The Mathematical Theory of Communication, Urbana: University of Illinois Press.

Southcott C B, Boyd I, Coleman A E & Hammett P G (1990). Low bit rate speech coding for practical applications. In C Wheddon and R Linggard (Eds), Speech and Language Processing, London: Chapman & Hall.

Spärck Jones K & Wilkes Y (Eds) (1985). Automatic Natural Language Parsing, Chichester: Ellis Horwood.

Storer J A (1988). Data Compression: Methods and Theory, Rockville, Maryland: Computer Science Press.

Sudkamp T A (1988). Languages and Machines, an Introduction to the Theory of Computer Science, Reading, Mass.: Addison-Wesley.

Von Békésy G (1967). Sensory Inhibition, Princeton, NJ: Princeton University Press.

Wallace C S & Boulton D M (1968). An information measure of classification. Computer Journal 11, 185-195.

Wallace C S & Freeman P R (1987). Estimation and inference by compact coding. Journal of the Royal Statistical Society B 49(3), 240-252.

Wolff J G (submitted for publication, a). Towards a new concept of software.

Wolff J G (submitted for publication, b). Computing as compression: SP20.

Wolff J G (1991a). Towards a Theory of Cognition and Computing, Chichester: Ellis Horwood.

Wolff J G (1991b). On the integration of learning, logical deduction and probabilistic inductive inference. Invited paper for the First International Workshop on Inductive Logic Programming, Vienna do Costello, Portugal, 1991.

Wolff J G & Chipperfield A J (1990). Unifying computing: inductive learning and logic. In the Proceedings of Expert Systems 90: T R Addis and R M Muir (Eds), Research and Development in Expert Systems VII, Cambridge: Cambridge University Press, pp 263-276.

Wolff J G (1990). Simplicity and power: some unifying ideas in computing. Computer Journal 33(6), 518-534. Reprinted in Chapter 4 of Wolff (1991a).

Wolff J G (1988). Learning syntax and meanings through optimization and distributional analysis. In Y Levy, I M Schlesinger and M D S Braine (Eds), Categories and Processes in Language Acquisition, Hillsdale, NJ: Lawrence Erlbaum. Reprinted in Chapter 2 of Wolff (1991a).

Wolff J G (1987). Cognitive development as optimization. In L Bolc (Ed), Computational Models of Learning, Heidelberg: Springer-Verlag, pp 161-205.

Wolff J G (1982). Language acquisition, data compression and generalization. Language & Communication 2, 57-89. Reprinted in Chapter 3 of Wolff (1991a).

Zipf GK (1949). Human Behaviour and the Principle of Least Effort, Cambridge, Mass.: Addison- Wesley.

Zipf (1935). The Psycho-Biology of Language: an Introduction to Dynamic Philology, Boston: Houghton Mifflin. Reprinted by the MIT Press (Cambridge, Mass., 1965).

FIGURE CAPTIONS

Figure 1. Variation in the rate of firing of a single ommatidium of Limulus in response to changing levels of illumination (Ratliff, Hartline & Miller, 1963, p 118).

Figure 2. Two sets of recordings from a single ommatidium of Limulus (Ratliff & Hartline, 1959, p 1248).

Figure 3. A random-dot stereogram (from Julesz, 1971, p 21).

Figure 4. Diagram to show the relationship between the left and right images in Figure 3 (based on Julesz, 1971, p 21).

Figure 5. A context-free phrase structure grammar.

Figure 6. A CF-PSG with recursion.

Figure 7. A query and database records to illustrate query-by-example.